- Identify the Problem Type
- Template for Common Algorithms
- Binary Search
- Sliding Window
- Depth First Search
- Cycle Detection in Directed Graph
- Topological Sort – Precedence-Constrained Scheduling
- Back-tracking
- Dynamic Programming
- Breath First Search
- Find Clusters in a Graph
- Prim's Algorithm (Find MST)
- Kruskal's Algorithm (Find MST)
- Dijkstra Algorithm (Shortest Path for positive weights)
- Bellman-Ford Algorithm (Shortest Path without negative cycles)
- Manipulating Data Structures
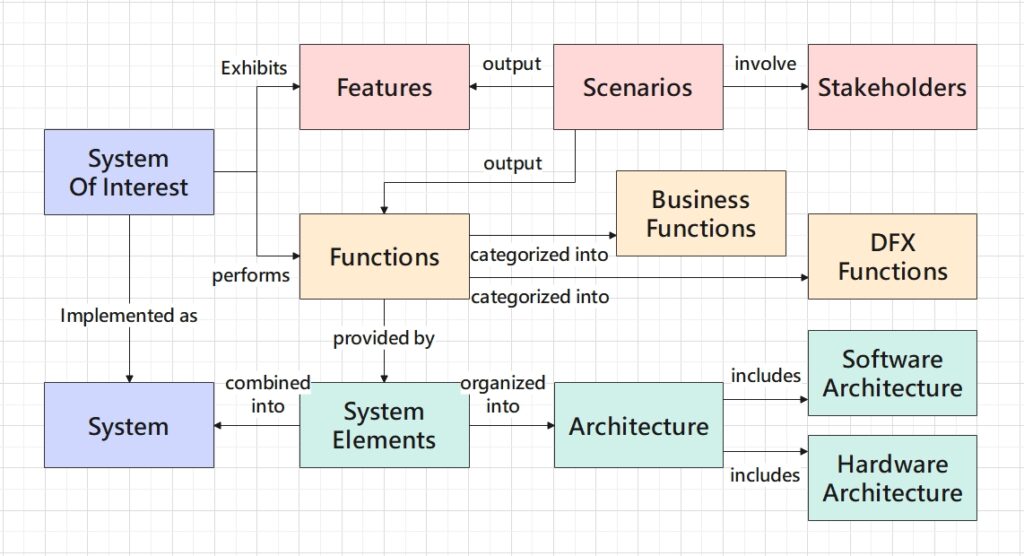
This article is an overview of the most common algorithms and data structures. Instead of explaining how each of these tools works, I aim at offering insights into what scenarios each algorithm can provide solution in, and what data structures enable each algorithm.

Identify the Problem Type
Search for the one input that makes the output optimal.
Given a monotonic relationship between an independent variable x and a dependent variable f(x), find the x which makes f(x) satisfy some conditions. -> Binary Search.
E.g. 1011. Capacity To Ship Packages Within D Days
Search for the range that makes the elements within it optimal.
Given an array, unsorted or sorted, find the optimum of a quantity related to a section of the array. -> Sliding Window.
E.g. 2009. Minimum Number of Operations to Make Array Continuous
Make a series of decisions to get the optimal outcome.
No Shortcut: All possible series need to be considered.
Model all possible series of decisions as a decision tree. Each node is the record of all previously made decisions (root node is an empty record), while each edge branching out from a node represents a possible decision from the remaining valid choices.
Optimal Sub-structure & Overlapping Sub-problems
If the solution to the original problem can be deduced from the solution(s) of one or more sub-problems (aka optimal sub-structure), then dynamic programming can be applied.
0/1 knapsack – choose a subset of items from all available items of limited quantity, so that the total weight falls within allowance, and the total value is maximized.
DP works because the max value for choosing from [i..n-1] items is either the max between (1) the max value for choosing from [i+1..n-1] and not including item i, and (2) the max value for choosing from [i+1..n-1] and including item i. In both cases, the weight constraint j for including item i or not should also be considered.
Unbounded knapsack – similar to 0/1 knapsack, but the quantity of each available item is unlimited.
Longest Common Sequence
Precedence-Constrained Scheduling
Given a directed graph, sort the order of the vertices such that all the directed edges point from a vertex earlier in the order to a vertex later in the order, or report that doing so is impossible (due to the presence of a cycle). –> Topological sort.
Find Clusters in a Graph
Given a graph, allocate a cluster id to each node, so that all nodes in the same cluster have the same cluster id.
928. Minimize Malware Spread II
Minimum Spanning Tree of Graph
Assume all nodes in a given graph is connected, find the minimum spanning tree which connects all the nodes with the shortest total edge weights.
-> Prim’s Algorithm
-> Kruskal’s Algorithm
1584. Min Cost to Connect All Points
Shortest Paths in Graph
Given a source node, find the shortest path from it to each of all other nodes in the graph.
Positive edge weights, can have cycles -> Dijkstra
Positive or negative edge weights, no negative cycles -> Bellman-Ford
787. Cheapest Flights Within K Stops
Template for Common Algorithms
Binary Search
Given a monotonic function f(x), move two pointers starting from the lower and upper bounds of x respectively towards the middle, i.e. move in opposite directions. Choose each move which makes f(x) closer to its target. At the end, both pointers are converged into the x where f(x) == target.
(For the case where multiple values of x satisfy the requirement and the smallest or largest satisfying x is desired, one of the pointers will continue to move even after it has pointed to a satisfying x. It will stop immediately after it has just moved past the optimal x.)
def binary_search(nums: List[int], target: int) -> int:
# prerequisite for binary search is monotonic function.
nums.sort()
# lower and upper bound of independent variable x, inclusive.
left = 0
right = len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
fx = f(mid, nums)
if fx == target:
return mid # Case 1. Find any satisfying x.
# right = mid - 1 # Case 2. Find smallest satisfying x.
# left = mid + 1 # Case 3. Find largest satisfying x.
elif fx > target: # need to decrease fx.
right = mid - 1 # for increasing f(x).
# left = mid + 1 # for decreasing f(x).
elif fx < target: # need to increase fx.
left = mid + 1 # for increasing f(x).
# right = mid - 1 # for decreasing f(x).
# Case 1. Find any satisfying x.
return -1
# Now left == right + 1.
# Case 2. Find smallest satisfying x.
# return left if f(x) == target else -1
# Case 3. Find largest satisfying x.
# return right if f(x) == target else -1int BinarySearch(vector<int>& nums, int target) {
// prerequisite for binary search is monotonic function.
sort(nums.begin(), nums.end());
// lower and upper bound of independent variable x, inclusive.
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) // 2;
int fx = f(mid, nums);
if (fx == target) {
return mid; // Case 1. Find any satisfying x.
// right = mid - 1; // Case 2. Find smallest satisfying x.
// left = mid + 1; // Case 3. Find largest satisfying x.
} else if (fx > target) { // need to decrease fx.
right = mid - 1; // for increasing f(x).
// left = mid + 1; // for decreasing f(x).
} else if (fx < target) { // need to increase fx.
left = mid + 1; // for increasing f(x).
// right = mid - 1; // for decreasing f(x).
}
# Case 1. Find any satisfying x.
return -1;
# Now left == right + 1.
# Case 2. Find smallest satisfying x.
# return f(left) == target ? left : -1;
# Case 3. Find largest satisfying x.
# return f(right) == target ? right : -1;
}Sliding Window
Move two pointers in the same direction from one end of an array to the other end.
The window width should be variable if the problem wants to find the maximum or minimum range meeting certain condition(s). The sliding window works as follows – With left unmoved, right will be responsible for expanding the window and find a valid window. Once the window becomes valid, right will stay at where it is, and left will be responsible for shrinking the window until the window is no longer valid. At this point, left and right will give a locally optimal window. right can expand the window again to start finding the next locally optimal window.
# Record data in window in a dict so as to ease access.
from collections import defaultdict
window = defaultdict(int) # {'element': count}
# Assistant data:
# If numbers of unique elements in window need to match some needs,
# the needs can be recorded in another dict for easy comparison.
need = defaultdict(int) # {'element': count}
# Then a counter can track how many unique elements in window have matched the needs.
valid = 0 # when valid == len(needs), try shrinking the window.
# locally optimal result will update the globally optimal.
best_left = 0
best_right = float('inf')
# window is array[left:right].
# left is always inclusive.
# right is inclusive before indexing, but exclusive afterwards.
left = 0
right = 0
while right < len(array):
# expand window
r = array[right] # access element before incrementing index right.
right += 1 # right has now gone beyond the window.
# add element into window if needed, and update assistant data.
if r in need:
window[r] += 1
if window[r] == need[r]:
valid += 1
while valid == len(need): # while window should be shrunk.
# Case 1: update result here if it is already valid before the window is shrunk.
if best_right - best_left > right - left:
best_left = left
best_right = right
# shrink window
l = array[left] # access element before incrementing index left.
left += 1
# remove data from window if it was recorded before.
if l in need:
# Update assistant data BEFORE the window.
if window[l] == need[l]:
valid -= 1
window[l] -= 1
# end of shrinking the window.
# Case 2: update result here if it is valid only after the window has been shrunk.
# max_length = max(max_length, right - 1 - (left - 1))
# right has reached the end of array. Now return final result.
if best_right == float('inf'):
return []
return array[best_left:best_right]unordered_map<char, int> need, window;
int valid = 0;
for (char c : t) {
need[c]++;
}
int bestLeft = 0, bestRight = INT_MAX;
int left = 0, right = 0;
while (right < s.size()) {
char r = s[right];
right++;
if (need.count(r)) {
window[r]++;
if (window[r] == need[r]) {
valid++;
}
}
// Contract window.
while (valid == need.size()) {
// Case 1: update result here if it is already valid before the window is shrunk.
if (bestRight - bestLeft > right - left) {
bestRight = right;
bestLeft = left;
}
char l = s[left];
left++;
if (need.count(l)) {
if (window[l] == need[l]) {
valid--;
}
window[l]--;
}
}
// Case 2: update result here if it is valid only after the window has been shrunk.
// max_length = max(max_length, right - 1 - (left - 1))
}
// valid substring is [bestLeft, bestRight).
return bestRight == INT_MAX ? "" : s.substr(bestLeft, (bestRight - bestLeft));The locally optimal result of the window can be updated in one of two positions in the code, marked as red above. The corresponding explanations are here:
- Case 1: update result before the window is shrunk if the result is already valid before so.
(Example Problem: LeetCode 76. Minimum Window Substring which aims to match all characters.
Shrink window after all characters have been matched, so as to remove redundant chars on the left.) - Case 2: update result after shrinking the window if the result is valid only after so.
(Example Problem: LeetCode 3. Longest Substring Without Repeating Characters which aims to find substring with no duplicate chars.
Shrink window after a duplicate has been found, so as to find the next substring with no duplicate chars.)
If each position in the array needs to be considered as the left pointer, and the window to be expanded by the right pointer, then it makes more sense to increment left in the outer while-loop.
Example 2009. Minimum Number of Operations to Make Array Continuous
changes = n # result to be minimized.
left = 0
right = 0
while left < len(sorted_unique_nums):
lower_bound = sorted_unique_nums[left]
upper_bound = lower_bound + (n-1) # inclusive
# Expand window.
while right < len(sorted_unique_nums) and sorted_unique_nums[right] <= upper_bound:
right += 1
changes = min(changes, n - (right-left))
left += 1
return changesint changes = n; // result to be minimized.
int left = 0;
int right = 0;
while (left < sortedUniqueNums.size()) {
int lowerBound = sortedUniqueNums[left];
int upperBound = lowerBound + (n-1); // inclusive.
// Expand window.
while (right < sortedUniqueNums.size() && sortedUniqueNums[right] <= upperBound) {
right += 1;
}
changes = min(changes, n - (right - left));
left += 1;
}
return changes;Depth First Search
Tree Traversal
For binary tree, we have three types of DFS traversal – pre-order, in-order and post-order. The comparison between their orders is as follows.

- pre-order (from top to bottom) – parent –> consecutive left child until left leaf –> right leaf
- in-order (from left to right) – left leaf –> parent –> right leaf –> grandparent
- post-order (from bottom to top) – left leaf –> right leaf –> parent
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def dfs(node: TreeNode) -> None:
# base case for recursion
if node is None:
return
# 1. pre-order operation
dfs(node.left)
# 2. in-order operation
dfs(node.right)
# 3. post-order operation
print(node.val)
root = TreeNode(1)
root.left = TreeNode(2)
root.left.left = TreeNode(3)
root.left.right = TreeNode(4)
root.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.left.left = TreeNode(7)
dfs(root)
# pre-order: 1 2 3 4 5 6 7
# in-order: 3 2 4 1 7 6 5
# post-order: 3 4 2 7 6 5 1struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
void DFS(TreeNode* node) {
// base case for recursion.
if (node == nullptr) {
return;
}
// 1. pre-order operation.
DFS(node->left);
// 2. in-order operation.
DFS(node->right);
// 3. post-order operation.
}Graph Traversal
visited = [False] * n
def dfs(u) -> None:
# Avoid revisiting a node. Possible when the graph is cyclic.
if visited[u]:
return
visited[u] = True
# Do whatever you want with the current node u here.
# For graph being adjacency list.
for v in graph[u]:
dfs(v)
# For graph being adjacency matrix.
# for v in range(n):
# if (graph[u][v] is not None): # edge u-v exists.
# dfs(v)
# Graph can contain disconnected clusters.
for u in range(n):
dfs(u)vector<bool> visited(n, false);
void dfs(int u) {
// Avoid revisiting a node. Possible even when the graph is acyclic.
if (visited[u]) return;
visited[u] = true;
// Do whatever you want with the current node u here.
// For graph being adjacency list.
for (int v : graph[u])
dfs(v);
// For graph being adjacency matrix.
// for (int v = 0; v < n; v++) {
// if (graph[u][v] != -1) // edge u-v exists.
// dfs(v);
// }
}
// Graph can contain disconnected clusters.
for (int u = 0; u < n; u++)
dfs(u);Cycle Detection in Directed Graph
How to determine a graph is cyclic?
Cycle has the characteristic that traversing on a path along it eventually ends up on a node previously met. Therefore, by keeping track of all the nodes met on the current path with an array on_path: List[bool], we can determine that a cycle does exist if we meet a node u which has on_path[u] == True, indicating node v have been met before.
Traversing the graph with DFS, before we move back up to the previous DFS level, on_path[u] for the current node u should be reset as False. In this way DFS continues with the correct record of what nodes are on the current path.
Deal with disconnected sub-graphs
Since a graph can consist of disconnected sub-graphs, it is necessary to start the traversal at each node. That is to perform traversal multiple times.
Performance Optimization

No matter a graph is cyclic or acyclic, there can be more than one path reaching a node u, as shown in the diagram above as the green and blue paths. Traversing on each path without any constraint will result in repeated traversal over all the nodes after u. Therefore, another array visited: List[bool] can be used to maintain whether each node has been visited. Once visited[u] is set as True, it won’t be reset as False. Immediately after it is set as True, all nodes subsequent to v will be traversed. So when v is revisited, all subsequent traversals can be skipped.
# n - total number of nodes
graph = [[] for _ in range(n)]
for u, v in edges: # edge u->v.
graph[u].append(v)
# Identify cycle by checking if node is already on the DFS path.
on_path = [False] * n
# Avoid repeated traversal from a visited node.
visited = [False] * n
has_cycle = False
# Logic for identifying a cycle, given a start node u.
def dfs(u: int) -> None:
if on_path[u]:
has_cycle = True
# return
# This if-condition of visited should be placed after
# if-condition of on_path, so that has_cycle can be set as True.
if visited[u] or has_cycle:
return
visited[u] = True
# Add current node onto the path before entering the next DFS level.
on_path[u] = True
for v in graph[u]:
dfs(v)
# Remove current node from path before returning to previous DFS level.
on_path[u] = False
# Deal with disconnected sub-graphs.
for u in range(n):
dfs(u)
print(f"Does the graph contain any cycle? {has_cycle}")# n - total number of nodes
vector<vector<int>> graph(n);
for (auto& edge : edges) { // edge u->v.
int from = edge[0];
int to = edge[1];
graph[from].emplace_back(to);
}
# Identify cycle by checking if node is already on the DFS path.
vector<bool> onPath(n, false);
# Avoid repeated traversal from a visited node.
vector<bool> visited(n ,false);
bool hasCycle = false;
// Logic for identifying a cycle, given a start node u.
void DFS(int u) {
if (onPath[u]) {
hasCycle = true;
}
// This if-condition of visited should be placed after
// if-condition of on_path, so that has_cycle can be set as True.
if (visited[u] || hasCycle) {
return;
}
visited[u] = true;
// Add current node onto the path before entering the next DFS level.
onPath[u] = true;
for (int v : graph[u]) {
DFS(v);
}
// Remove current node from path before returning to previous DFS level.
onPath[u] = false;
}
// Deal with disconnected sub-graphs.
for (int u = 0; u < n; u++)
DFS(u);
printf("Does the graph contain any cycle? %s", has_cycle ? "Yes" : "No");Record the nodes in each cycle
Apart from the array on_path, add another array path to the backtracking procedure, so that each node chosen can also be added and removed from the record path.
cycles: List[List[int]] = [] # Record each cycle as a list of nodes.
def dfs(u: int, path: List[int]):
if on_path[u]:
# Add cycle to `cycles`.
# Note: path here only contains one u (appended when first met).
# u has not been appended the second time.
cycle = [u]
for i in range(len(path) - 1, -1, -1):
cycle.append(path[i])
if path[i] == u:
break
cycle.reverse()
cycles.append(cycle)
return
if self.visited[node]:
return
self.visited[node] = True
path.append(u)
onPath[u] = True
for child in self.graph[u]:
self.dfs(path, child)
onPath[u] = False
path.pop()Topological Sort – Precedence-Constrained Scheduling
graph # Adjacency List.
n # number of nodes.
def __init__(self):
self.visited = [False] * n
self.onPath = [False] * n # Key for identifying a cycle.
self.hasCycle = False
self.sequence = [] # Record the topological order of the nodes.
def findOrder(self, n: int) -> List[int]:
# Start with each node. Each visited node won't be traversed again.
for i in range(n):
self.dfs(i) # May set hasCycle as True.
if self.hasCycle:
return []
self.sequence.reverse()
return self.sequence
def dfs(self, u):
if self.onPath[u]:
self.hasCycle = True
return
# avoid infinite recursion
if self.visited[u] or self.hasCycle:
return
self.visited[u] = True
self.onPath[u] = True
for v in self.graph[u]:
self.dfs(v)
self.onPath[u] = False
# Record post-order so that child nodes (dependent nodes)
# are appended first before the nodes being depended on.
# Reversing the entire sequence at the end gives the topological order.
self.sequence.append(u)Back-tracking

Add & Remove the Current Decision
Having define each decision as an edge of a decision tree, find all possible series of decisions by:
- Traverse the tree (in DFS manner),
- Record each decision when moving down, and remove the decision when moving up.
- Upon reaching a leaf node, copy the current series of decisions to the final result, then return and continue the DFS traversal.
results = []
def backtrack(path: List[], choices: Set[]):
# Record a result every time a last choice has been made.
if len(choices) == 0:
results.append(path.copy())
return
# Choose from remaining choices.
# Note: The order of choices to be iterated should not be changed,
# hence make a copy list(choices).
for c in list(choices):
# Make the current choice c.
path.append(c)
choices.remove(c)
backtrack(path, choices)
# Revert the current choice c.
path.pop()
choices.add(c)Decisions as Edges instead of Nodes
In a DFS in which the current path of traversal needs to be recorded, the current source node u of edge u->v is added to the record before iterating over each adjacent node v, and removed from the record after all iterations have completed. See the previous section about Cycle Detection for example:
def dfs(u):
...
on_path[u] = True
for v in graph[u]:
dfs(v)
on_path[u] = FalseThe underlying principle is that when the nodes instead of the edges are to be recorded, we record the source node u on each recursion level, so that the root node won’t be missed out. In other words, a DFS problem define the node as the decisions to be made.
In contrast, in a back-tracking problem, the edges are defined as the decisions to be made, while the nodes are the resulting set of previous decisions. Hence, on each recursion level, the record on an edge must be added and removed inside each iteration. Outside the iteration the edges are not accessible.
def backtrack():
...
for c in list(choices):
path.append(c)
choices.remove(c)
backtrack(path, choices)
path.pop()
choices.add(c)Dynamic Programming
0/1 Knapsack:
dp[i][j] = optimal result for reaching constraint j by considering all choices in coins[i:]. Note that considering a choice doesn’t mean the choice must be included.
The final required result is dp[0][W], where j=W is the original constraint.
dp[i][j] = optimal(dp[i-1][j], dp[i-1][j-weight_i] + price_i)
Unbounded Knapsack
dp[i][j] = optimal(dp[i-1][j], dp[i-1][j-weight_i] + price_i)
Breath First Search
Tree Traversal
from collections import deque
def bfs(root: TreeNode):
# edge case
if root is None:
return
queue = deque()
queue.append(root)
depth = 0
while (queue):
# Do what is needed for each level here.
print(f"depth: {depth}")
print(f"nodes: [", end=" ")
# Get the number of nodes on the current tree/graph level only,
# so that adding the nodes on next level to the queue won't affect the iteration on the current level.
for i in range(len(queue)):
node = queue.popleft()
# Do what is needed for each node here.
print(node.val, end=" ")
# Add nodes on next level to the queue.
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
depth += 1
print("]\n----")
# queue is now empty.
return#include <queue>
void BFS(TreeNode* root)
{
// Edge case.
if (root == nullptr) {
return;
}
queue<TreeNode*> q({root});
while (!q.empty()) {
// Obtain sz before for-loop because q.size() changes in each iteration.
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode* node = q.front();
q.pop();
if (node->left != nullptr) {
q.emplace(node->left);
}
if (node->right != nullptr) {
q.emplace(node->right);
}
}
}
}Graph Traversal
visited = [False] * n
def bfs(root) -> None:
queue = deque([root]) # same as queue = deque(); queue.append(root)
visited[root] = True
while queue:
u = queue.popleft()
# For graph being adjacency list.
for v in graph[u]:
if not visited[v]:
visited[v] = True
# Do whatever you want with node u here.
queue.append(v)
# For graph being adjacency matrix.
# for v in range(n):
# if (graph[u][v] is not None) \ # edge u-v exists.
# and (not visited[v]): # node v has not been visited.
# visited[v] = True
# queue.append(v)
# Graph can contain disconnected clusters.
for u in range(n):
bfs(u)vector<bool> visited(n, false);
void bfs(int root) {
queue<int> q({root});
visited[root] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
// For graph being adjacency list.
for (int v : graph[u]) {
if (!visited[v]) {
visited[v] = true;
// Do whatever you want with node u here.
q.emplace(v);
}
}
// For graph being adjacency matrix.
// for (int v = 0; v < n; v++) {
// if (graph[u][v] != -1 // edge u-v exists.
// && !visited[v]) { // node v has not been visited.
// visited[v] = true;
// q.emplace(v);
// }
// }
}
}
// Graph can contain disconnected clusters.
for (int u = 0; u < n; u++) {
bfs(u);
}Find Clusters in a Graph
BFS starting from each node
Node-indexed array to record the cluster id for each node.
BFS to assign cluster id to each node, one cluster at a time.
# adjacency matrix n x n. graph[u][v] == 1 if nodes u and v are connected.
graph
idx = 0 # Current cluster id, starts at 0.
# Start BFS from each node 'root', so that we don't miss out any cluster.
for root in range(n):
if ids[root] is not None: # visited.
continue
ids[root] = idx
q = deque([root])
while q:
u = q.popleft()
# Add all unvisited, adjacent nodes of u into the queue.
for v in range(n):
if graph[u][v] == 1 and ids[v] != idx:
# ('ids[v] != idx' is the same as 'ids[v] is None' here.)
ids[v] = idx
q.append(v)
idx += 1// adjacency matrix n x n. graph[u][v] == 1 if nodes u and v are connected.
vector<vector<int>> graph = ...;
int idx = 0; # Current cluster id, starts at 0.
# Start BFS from each node 'root', so that we don't miss out any cluster.
for (int root = 0; root < n; root++) {
if (ids[root] != -1) // visited.
continue;
ids[root] = idx;
queue<int> q({root});
while (!q.empty()) {
int u = q.front();
q.pop();
// Add all unvisited, adjacent nodes of u into the queue.
for (int v = 0; v < n; v++) {
if (graph[u][v] == 1 && ids[v] != idx) {
// ('ids[v] != idx' is the same as 'ids[v] is None' here.)
ids[v] = idx;
q.emplace(v);
}
}
}
idx += 1;
}Union-Find to union two nodes on each edge
Parent-link representation of the nodes stores information about the nodes in a different perspective from the original graph. In the original graph, cycles can exist in each cluster. In contrast, parent-link puts all nodes from the same cluster onto the same tree. The exact structure of the parent-link tree doesn’t matter, but by definition of a tree no cycles can exist. The height of the tree should be minimized to allow fast access to the tree root.
The fact that a node is the parent of another node in the parent-link representation does NOT mean that the two nodes are connected directly by an edge in the original graph.
class UF:
def __init__(self, n: int):
# Initialize unique cluster id to every node.
self.parent = [i for i in range(n)]
# Number of clusters may be less than n.
self.num_clusters = n
def union(self, p: int, q: int) -> None:
"""
Given two nodes in the same cluster, get their roots in parent-link,
and connect them to merge two trees into one.
"""
root_p = self.find(p)
root_q = self.find(q)
if root_p == root_q:
return
self.parent[root_q] = root_p
self.num_clusters -= 1
def find(self, x: int) -> int:
"""
Goals:
1. Return the root of node x.
2. SET the parent of every node in the chain from x to root AS the root.
"""
# Base case of recursion - the root is found.
if self.parent[x] == x:
return x
# Recursively find the root of x.
root = self.find(self.parent[x])
self.parent[x] = root # Goal 2.
return root # Goal 1.
def get_num_clusters(self) -> int:
return self.num_clustersclass UF {
private:
vector<int> parent;
int numClusters;
public:
UF(int n) {
// Initialize unique cluster id to every node.
parent = vector<int>(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
// Number of clusters may be less than n.
numClusters = n;
}
void Union(int p, int q) {
/*
Given two nodes in the same cluster, get their roots in parent-link,
and connect them to merge two trees into one.
*/
int root_p = Find(p);
int root_q = Find(q);
if (root_p == root_q) {
return;
}
parent[root_q] = root_p;
numClusters -= 1;
}
int Find(int x) {
/*
Goals:
1. Return the root of node x.
2. SET the parent of every node in the chain from x to root AS the root.
*/
// Base case of recursion - the root is found.
if (parent[x] == x)
return x;
// Recursively find the root of x.
int root = Find(parent[x]);
parent[x] = root; // Goal 2.
return root; // Goal 1.
}
int GetNumClusters() {
return numClusters;
}
}; // end of class.Prim’s Algorithm (Find MST)
BFS with Priority Queue to find the first n-1 shortest crossing edges. A crossing edge u-v satisfies the simple requirement that the new node v is not yet present in the MST.

If an edge ?-u has u already in the MST, adding this edge to the MST would have introduced a cycle in the MST, as shown by any gray edge in the diagram above.
When adding an edge u-v to the pq, we have no idea if this edge should be added to the MST. It is only when it pops out from the the pq can we decide if it belongs to the MST, with the aid of the flag in_mst[?]. in_mst[u] tells us if node u has already been added to the MST.
graph # n x n adjacency matrix
n = len(graph)
# Record which node v has been added to MST, so that
# other edges towards v won't be added to MST.
in_mst = [False] * n
# When in_mst[v] for all v is true, i.e. mst_nodes == n,
# the mst has been found, and algorithm can terminate before pq is empty.
mst_nodes = 0
weight_sum = 0
# Sometimes not only the total weight is sought for by the problem.
# The exact edges can be also sought for.
adj_edges = defaultdict(list)
# adj_edges[u] is a list of MST edges (weight, v) adjacent to u.
# Each element in pq is (weight, u, v) where weight is the priority.
pq = PriorityQueue()
pq.put((0, 0, None)) # (weight_u, u, parent in MST)
while not pq.empty():
weight_u, u, parent = pq.get()
# Ensure that no cycle (redundant edge to u) is added to MST.
if in_mst[u]:
continue
# Add current edge and node u to the MST.
in_mst[u] = True
weight_sum += weight_u
if parent is not None:
adj_edges[parent].append((weight, u))
# Early termination after all nodes have been added to the MST.
mst_nodes += 1
if mst_nodes == n:
break
# BFS: Add to the pq all eligible edges searched from u.
for v, weight_v in enumerate(self.graph[u]):
if u == v:
continue
if self.in_mst[v]:
continue
pq.put((weight_v, v, u))
print(weight_sum)
print(adj_edges)vector<vector<int>> graph; # n x n adjacency matrix
int n = graph.size();
// Record which node v has been added to MST, so that
// other edges towards v won't be added to MST.
vector<int> in_mst(n, false);
// When in_mst[v] for all v is true, i.e. mst_nodes == n,
// the mst has been found, and algorithm can terminate before pq is empty.
int mst_nodes = 0;
int weight_sum = 0;
// Sometimes not only the total weight is sought for by the problem.
// The exact edges can be also sought for.
unorder_map<int, vector<int>> adj_edges;
// adj_edges[u] is a list of MST edges (weight, v) adjacent to u.
struct State {
int weight;
int node;
int parent; // -1 means no parent node.
bool operator<(const State& state) const {
// "greater" comparison gives a min-heap.
return weight > state.weight;
}
};
// Each element in pq is (weight, u, v) where weight is the priority.
priority_queue<State> pq;
pq.push(State{0, 0, -1}); // (weight_u, u, parent in MST)
while (!pq.empty()) {
const State state = pq.top();
pq.pop();
int weight_u = state.weight;
int u = state.node;
int parent = state.parent;
// Ensure that no cycle (redundant edge to u) is added to MST.
if (in_mst[u]) continue;
// Add current edge and node u to the MST.
in_mst[u] = true;
weight_sum += weight_u;
if (parent != -1)
adj_edges[parent].push_back({weight, u});
// Early termination after all nodes have been added to the MST.
mst_nodes += 1;
if (mst_nodes == n)
break;
// BFS: Add to the pq all eligible edges searched from u.
for (int v = 0; v < n; v++) {
int weight_v = graph[u][v];
if (u == v)
continue;
if (in_mst[v])
continue;
pq.push(State{weight_v, v, u});
}
} // end of while.
// res: weight_sum, adj_edgesKruskal’s Algorithm (Find MST)
First sort all edges according to their weights.
Then find the first n-1 shortest edges u-v for which nodes u and v are not yet in the same cluster. Keeping track of the cluster information is achieved by the Union-Find data structure.

Adding an edge to the MST allows us to connect two nodes which are next to each other. These two nodes can originally belong to two disconnected clusters, as shown by the gray and while nodes in the diagram above. To form an MST with these two clusters, the shortest crossing edge between them should be chosen.
On the other hand, an edge should not be added to the MST if the two nodes of the edge have already belonged to the same cluster. Adding this edge would introduce a cycle to the MST.
class Kruskal:
def __init__(self, n: int, sorted_edges: List[List[int]]) -> None:
self.sorted_edges = sorted_edges
# Initialize UF with number of clusters equal to number of nodes.
self.uf = UF(n)
self.weight_sum = 0
# Sometimes not only the total weight is sought for by the problem.
# The exact edges can be also sought for.
self.mst_edges = [] # Each element is an MST edge (weight, u, v).
self.build_mst()
def get_mst_weight(self) -> int:
return self.weight_sum
def build_mst(self) -> None:
for weight, u, v in self.sorted_edges:
# Early termination after all nodes have been added to the MST.
if self.uf.get_num_clusters() == 1:
break
if self.uf.connected(u, v):
# Nodes u and v are already in MST.
# Skip this non-optimal edge.
continue
# Add the current minimum edge to the MST.
self.weight_sum += weight
self.mst_edges.append((weight, u, v))
self.uf.union(u, v)
assert self.uf.get_num_clusters() == 1class Kruskal {
private:
vector<vector<int>> sorted_edges;
UF uf;
int weight_sum = 0;
// Sometimes not only the total weight is sought for by the problem. The exact edges can be also sought for.
vector<vector<int>> mst_edges;
// Each element is an MST edge (weight, u, v).
public:
Kruskal(int n, vector<vector<int>> edges]) : {
sorted_edges = edges;
// Initialize UF with # of clusters equal to # of nodes.
uf = UF(n);
build_mst();
}
int get_mst_weight() const {
return weight_sum;
}
void build_mst() {
for (auto& edge : sorted_edges) {
int weight = edge[0];
int u = edge[1];
int v = edge[2];
// Early termination after all nodes have been added to the MST.
if (uf.GetNumClusters() == 1)
break;
if (uf.Connected(u, v)) {
// Nodes u and v are already in MST.
// Skip this non-optimal edge.
continue;
}
// Add the current minimum edge to the MST.
weight_sum += weight;
mst_edges.push_back({weight, u, v});
uf.Union(u, v);
}
// assert self.uf.get_num_clusters() == 1
}
}; // end of class.Dijkstra Algorithm (Shortest Path for positive weights)
Starting from the given source node, perform BFS, and sort the nodes in each BFS level according to its shortest distance from the source. The sorting is done by a priority queue. Each state (distance, node_index[, stop]) put into the priority queue represents a path reaching the corresponding node.
Dijkstra works because the sorting on each BFS level has led to that the state popped from the queue every time has the current shortest distance.
Example problem: 743. Network Delay Time
If extra constraint such as the number of intermediate nodes stop is present in the shortest path search problem (E.g. 787. Cheapest Flights Within K Stops), then the following important pieces of code will have to be ensured:
- On each BFS level, each state for node v should be added to the priority queue, instead of just the state for node v with the current shortest path towards v. (This is because the shortest path towards v may have met the limit of the extra constraint. So it can’t give the shortest path towards its next node.)
- When calculating the distance towards the next node v, make sure to use the distance towards u stored in the current state for u, instead of the current shortest distance to u. (Because the shortest distance may not match the current path.)
- Update the constraining variable in each state, so that any state violating the constraint will be filtered out after having been popped from the pq.
- Optimize the shortest path search by realizing that for the same v, any state with longer distance and less room for the constraint won’t give any optimal solution for later nodes. Hence, no need to add these states to the queue.
# ignore `shortest_paths[0]` because node index starts from 1.
shortest_paths = [float('inf')] * (n + 1)
# Initialize stops with inf because optimization skips stop_v > stops[v].
stops = [float('inf')] * (n + 1)
# Adjacency List where edges[u] is a list of all nodes v pointed to by u.
# w is the weight of edge u->v.
edges = defaultdict(list)
for u, v, w in times:
edges[u].append((v, w))
# Record candidate nodes.
pq = PriorityQueue()
# Initialize solution at source node src. Travel to src requires 0 distance.
shortest_paths[src] = 0
# State is (distance, node index, stop).
# (initialize stop == -1 so that second vertex will have stop == 0, third vertex will have stop == 1.)
pq.put((0, src, -1))
# BFS until all edges have been traversed.
while not pq.empty():
distance_u, u, stop_u = pq.get()
# Can return early if the problem only requires distance to a particular destination.
# if u == dst:
# return distance_u
# Unconstraint case only: Filter out any ?->u choices if the best ?->u has been found.
# if distance_u > shortest_paths[u]:
# continue
if stop_u >= max_stop:
continue
for v, w in edges[u]:
# Do not use shortest_paths[u] here.
distance_v = distance_u + w
stop_v = stop_u + 1
# Check whether reaching v from u gives a better result.
if shortest_paths[v] > distance_v:
shortest_paths[v] = distance_v
stops[v] = stop_v
# Unconstraint case: choose u->v as the new best edge to reach v.
# pq.put((distance_v, v))
# Other choices ?->v existing in pq will be filtered out.
# Careful not to condition on (distance_v == shortest_paths[v] and stop_v == stops[v]), as it will disable state of v from entering the pq.
if distance_v > shortest_paths[v] and stop_v > stops[v]:
continue
# Constraint case: consider every path to v for the next nodes.
pq.put((distance_v, v, stop_v)) struct State {
int id;
int dist;
int stop;
bool operator<(const State& state) const {
// "greater" comparison gives a min-heap.
return dist > state.dist;
}
};
vector<int> distTo(n, INT_MAX);
distTo[src] = 0;
vector<int> stop(n, INT_MAX);
stop[src] = -1;
priority_queue<State> pq;
pq.push(State{src, 0, -1});
while (!pq.empty()) {
// WARN: Do not define `state` as reference to pq.top() here, because it will change after pq.pop().
const State state = pq.top();
pq.pop();
int u = state.id;
int distToU = state.dist;
int stopU = state.stop;
// Do not return early here if shortest path to every node is required.
if (u == dst)
return distTo[u]; // or distToU.
if (stopU == k)
continue;
int stopV = stopU + 1;
for (auto& adj : graph[u]) {
int v = adj.first;
int w = adj.second;
int distToV = distToU + w;
if (distTo[v] > distToV) {
distTo[v] = distToV;
stop[v] = stopV;
// pq.push(State{v, distToV, stopV});
}
if (distToV > distTo[v] && stopV >= stop[v])
continue;
pq.push(State{v, distToV, stopV});
}
}
return -1;Bellman-Ford Algorithm (Shortest Path without negative cycles)
Find shortest paths from a given source.
Maintain a node-indexed array dist_to: List[int] which records the shortest distances from the given source to all other nodes. dist_to[src] is initialized as 0 while all other distances are initialized as positive infinity.
dist_to = [float('inf')] * V
dist_to[src] = 0vector<int> distTo(V, INT_MAX);
distTo[src] = 0When a node is later found to be unreachable from the source, its distance will remain as positive infinity. On the other hand, some nodes are reachable from the source, but the path from the source to each of those nodes contains a negative cycle. In this case, the distance of this kind of nodes will be set as negative infinity at the end of the algorithm.
Bellman-Ford Algorithm works as follows:
- Consider the edges in any order. Relax all of them, i.e. update the distance of a node if reaching it from an edge gives a shorter distance.
- Repeat step 1 to make V-1 such passes in total, where V is the total number of nodes in the graph. (V-1 is the maximum number of edges needed to reach any node from the source.)
In order to keep track of the nodes in all shortest paths, maintain another node-indexed array parent: List[int] . parent[v] of node v is the node index u for directed edge u->v involved in the shortest path to v.
parent = [None] * V
passes = V - 1
for _ in range(passes):
# In the current pass, update a clone instead of the result from the previous pass, so that dist_to[u] won't be updated.
# That is, each pass only moves each node to its adjacent nodes.
clone = dist_to.copy()
for u, v, dist in edges: # dist is the weight of edge u->v.
# Update clone from dist_to[u] and current edge weight.
dist_to_v = dist_to[u] + dist
if clone[v] > dist_to_v:
clone[v] = dist_to_v;
parent[v] = u
dist_to = clone
return dist_tovector<int> parent(V, -1); // Default value -1 is simply a placeholder.
for (int k = 0; k < V-1; k++) {
vector<int> clone(distTo.begin(), distTo.end());
for (auto& time : times) {
int u = time[0];
int v = time[1];
int w = time[2];
if (distTo[u] != INT_MAX) {
int distToV = distTo[u] + w;
if (clone[v] > distToV) {
clone[v] = distToV;
parent[v] = u;
}
}
}
distTo = clone;
}
// Retrieve the path from src to any node x.
vector<int> path{x};
int u = x;
while (u != src) {
u = parent[u];
path.emplace_back(u);
}
reverse(path.begin(), path.end());Illustration of the necessity of the clone.
Bellman-Ford – Cheapest Flights within K Stops – Leetcode 787 – Python
Proof by induction that after the i-th pass Bellman-Ford computes a shortest path towards a node reachable through at maximum i number of edges from the source.
Consider a specific shortest path: src -> v_1 -> v_2 -> … -> v_i -> v_{i+1}. Vertex v_i may be reached by another path with less than i edges. Here we shall prove that after i passes of relaxing all edges, the shortest path must have been found, either as our specific path or not.
Base case: When i = 0 (no edge from source), travelling to source takes 0 total distance.
Assumption: After i passes of relaxing all edges, src -> v_1 -> v_2 -> … -> v_i (with i edges from source) is a shortest path from source to v_i, and dist_to[v_i] is its length.
Induction: By relaxing all edges one more time, the distance from source to v_i then to v_{i+1} is found. The shortest distance to v_{i+1} is either dist_to[v_i] + dist of ‘edge v_i -> v_{i+1}’, or some previously computed shortest distance of a path with less than i+1 edges. Either way, as long as v_{i+1} won’t be reachable through a path with more than i+1 edges from the source, the shortest distance to v_{i+1} is found.
Conclusion: By relaxing all edges K times, the shortest distances towards any nodes reachable through at max K edges from the source have been found.
Find a negative cycle.
Reference: https://cp-algorithms.com/graph/bellman_ford.html
If there exists a negative cycle, an extra V-th pass of relaxing all edges will lead to a further decrease in the distance to any node which either lies in a negative cycle or is reachable from the negative cycle.
To identify a negative cycle (the nodes lying in it), start from any node x which has its distance further decreased in the V-th pass. In order to find a node y guaranteed to lie in a negative cycle, set y as the (V-1)-th predecessor of x, because any source node including those in a negative cycle must not travel via more than V-1 edges in order to reach x.
After find node y in a negative cycle, simple iterate over its predecessors until a predecessor is y itself. These predecessors are obviously all the nodes forming the current negative cycle. (Take special care for negative-weight self-loop.)
x = None # index of node with distance of negative infinity.
# The V-th pass to check for further decrease in distance(s).
clone = dist_to.copy()
for u, v, dist in edges:
dist_to_v = dist_to[u] + dist
if dist_to_v < clone[v]:
clone[v] = - float('inf')
x = v
dist_to = clone
# Find node y which is guaranteed to lie in a negative cycle.
if x is None:
# No distance has further decreased in the V-th pass.
print("Negative cycle doesn't exist in the graph.")
else:
y = x
for _ in range(V-1):
y = parent[y]
# Now y is guaranteed to lie in a negative cycle.
# Find all nodes in that negative cycle.
if y == parent[y]:
print("node y has a negative-weight self-loop.")
else:
cycle = [y]
u = parent[y]
while u != y:
cycle.append(u)
u = parent[u]
cycle.reverse()
print(f"Negative cycle is {cycle}.")The code above finds one negative cycle, even though multiple negative cycles may exist in the graph. Moreover, the code only finds a negative cycle reachable from the chosen source node. In a graph containing disconnected clusters, there can be negative cycles which a chosen source node cannot reach.
In order to find any negative cycle, initialize distance to each node as zero but not positive infinity – as if we are looking for the shortest path from all vertices simultaneously. The logic for the V-th pass and the retrieval of a negative cycle remains unchanged.
dist_to = [0] * VFinally, in order to find all negative cycles, we can record all nodes x which have their distances decreased in the V-th pass. By finding the negative cycles corresponding to each x, and eliminating repeated cycles, all negative cycles can be found.
Manipulating Data Structures
Vector
list1 = [(6, 'c'), (4, 'a'), (5, 'b')]
# len(list1) == 3.
# Return new sorted array.
sorted_list = sorted(list1, key=lambda x: x[0], reverse=True)
# sorted_list: [(6, 'c'), (5, 'b'), (4, 'a')], original list is not sorted.
# In-place sorting.
list1.sort(key=lambda x: x[0], reverse=True)#include <algorithm> // std::max_element, std::sort
#include <numeric> // std::accumulate
vector<int> v1{1,2,3,4};
// v1.size() == 4.
// Find max element via max_element.
std::vector<int>::iterator maxIt = max_element(v1.begin(), v1.end());
cout << "max element has value " << *maxIt << " and index "
<< distance(v1.begin(), maxIt) << endl;
// Similar for min_element.
// Find sum of elements.
// Note that the third argument (initial value) cannot be omitted.
int sum = accumulate(v1.begin(), v1.end(), 0);
// Sort vector in-place, in descending order.
sort(v1.begin(), v1.end(), greater<int>());# 2D array.
rows = 2
columns = 3
dp = [[0] * columns for _ in range(rows)]
"""
dp: [[0,0,0]
[0,0,0]]
"""// 2D array.
row = 2
col = 3
vector<vector<int>> dp(row, vector<int>(col, 0));
/*
dp: {{0,0,0},
{0,0,0}}
*/Linked List
#include <list>
list<char> li;
li.emplace_back('a');
li.emplace_back('b');
list<char>::iterator bIt = std::prev(li.end());
li.emplace_back('c');
li.insert(bIt, 'd'); // insert 'd' before 'b'.
li.erase(bIt); // remove 'b' via its iterator.
for (auto it = li.begin(); it != li.end(); it++) {
cout << *it << endl;
}
/*
print:
a
d
c
*/Queue (First-In-First-Out)
from collections import deque
queue = deque()
queue.append((4, 'a'))
queue.append((5, 'b'))
obj = queue.popleft()
# obj: (4, 'a')
# deque has no empty() method, unlike PriorityQueue which has.
while queue:
queue.popleft()#include <queue>
queue<int> q({1,2,3});
q.emplace(4);
q.emplace(5);
int val = q.front();
q.pop(); // return void.
while (!q.empty()) {
....
}Stack (Last-In-First-Out)
from collections import deque
stack = deque()
stack.append((4, 'a'))
stack.append((5, 'b'))
obj = stack.pop()
# obj: (5, 'b')
# deque has no empty() method, unlike PriorityQueue which has.
while stack:
stack.pop()#include <stack>
stack<int> = s({1,2,3});
s.emplace(4);
s.emplace(5);
int val = s.top();
s.pop(); // return void.
while (!s.empty()) {
...
}Dictionary / Hashmap
dict1 = {'a': 4, 'b': 5, 'c': 6}
for key, value in dict1.items():
print(f"key = {key}, value = {value}")
if 'b' in dict1:
print(dict['b'])unordered_map<char, int> m;
// Each element has default value corresponding to its data type.
// E.g. int has default value 0.
string s = "chon hei lam";
for (char c : s) {
m[c]++;
}
// Iterate elements in a map.
for (auto it = m.begin(); it != m.end(); it++) {
cout << "key: " << it->first << ", value: " << it->second << endl;
}
// Two ways to check the existence of a key.
char key = 'h';
// map::count(key) which returns 1 (present) or 0 (absent).
if (m.count(key) == 1) {
cout << key << " exists in map.\n";
}
auto it = m.find(key);
if (it != m.end()) {
cout << key << " exists in map.\n";
}Set
set1 = set() # WARN: {} is initialized as a dictionary.
set1.add((4, 'a'))
set1.add((5, 'b'))
set1.add((6, 'c'))
set1.remove((6, 'c')) # remove a specific item.
obj = set.pop() # remove a random item.set<int> s({-1,2}); // or set<int> s = {-1,2};
s.insert(1);
s.insert(-10);
if (s.count(-10) == 1) {
// value -10 exists in the set.
}
size_t numElementsErased = s1.erase(-10);
// numElementsErased == 0 if -10 doesn't exist in the set originally.
int value = -1;
auto it = s.find(value);
if (it != s.end()) {
printf("value %d exists in the set.", value);
}# set can be used to remove duplicates -> O(n).
no_duplicates = set([(7, 'd'), (6, 'c'), (6, 'c')])
# sorted() will implicitly convert a set into a list.
list_no_duplicates = sorted(no_duplicates)// Given an unsorted vector nums with duplicated elements, remove duplicates and sort the remaining elements.
// Remove duplicates.
unordered_set<int> unique(nums.begin(), nums.end());
// Sort the new array with unique numbers.
vector<int> sortedUniqueNums(unique.begin(), unique.end());
sort(sortedUniqueNums.begin(), sortedUniqueNums.end());Tree
class TreeNode():
"""
# Binary Tree:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
# N-ary Tree:
def __init__(self, val=0):
self.val = val
self.children = []
# A child can be added by children.append(TreeNode(x)).struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};Graph
There are two forms of data structures to represent a graph, namely an adjacency list and an adjacency matrix. The list form records only the adjacent nodes of each node, so takes up less memory. In contrast, the matrix form takes up n*n memory, but allow direct access to the data of the edge u->v through matrix[u][v].
# Adjacency List
# 1. Initialization
# n - total number of nodes. Index starts at 0.
graph = [[] for _ in range(n)]
# Alternative to list is dict.
from collections import defaultdict
graph = defaultdict(list)
for u, v, w in edges: # directed edge u->v with weight w.
graph[u].append((v, w))
# 2. Access adjacent nodes of node u.
for v, w in graph[u]: # graph[u] is the list of adjacent nodes.
print(v, w)// Adjacency List
// 1. Initialization
// n - total number of nodes. Index starts at 0.
vector<vector<pair<int, int>>> graph(n);
for (auto& edge : edges) { // directed edge u->v with weight w.
int u = edge[0];
int v = edge[1];
int w = edge[2];
graph[u].push_back({v, w});
}
// 2. Access adjacent nodes of node u.
for (auto& adj : graph[u]) { // graph[u] is the list of adjacent nodes.
int v = adj.first;
int w = adj.second;
printf("%d %d", v, w);
}# Adjacency Matrix
# 1. Initialization
graph = [[None] * n for _ in range(n)]
for u, v, w in edges:
graph[u][v] = w
# 2. Access adjacent nodes of node u.
for v, w in enumerate(graph[u]):
print(v, w)
# 3. Direct access to edge u->v.
print(graph[u][v])
# 4. Find all adjacent nodes of u, by iterating all nodes in the graph.
for v in range(n):
if (u != v) and (graph[u][v] is not None):
print(v)// Adjacency Matrix
// 1. Initialization
vector<vector<int>> graph(n, vector<int>(n, -1));
for (auto& edge : edges) { // directed edge u->v with weight w.
int u = edge[0];
int v = edge[1];
int w = edge[2];
graph[u][v] = w;
}
// 2. Access adjacent nodes of node u.
for (int v = 0; v < graph[u].size(); i++) {
int w = graph[u][v];
printf("%d %d", v, w);
}
// 3. Direct access to edge u->v.
printf("%d", graph[u][v]);
// 4. Find all adjacent nodes of u, by iterating all nodes in the graph.
for (int v = 0; v < n; v++) {
if ((v != u) && graph[u][v] != -1) {
printf("%d ", v);
}
}Priority Queue / Heap
from queue import PriorityQueue
pq = PriorityQueue() # min-heap by default.#include <queue>
#include <functional>
priority_queue<int> maxPQ; // max-heap by default.
priority_queue<int, vector<int>, greater<int>> minPQ;# Usage 1 - Use tuple to store priority and data.
pq.put((5, 'a')) # 5 is the priority and 'a' is the data.
pq.put((1, 'c'))
pq.put((1, 'b'))
# `while pq` will not terminate. `pq.empty()` must be used.
while not pq.empty():
print(pq.get())
"""
print:
(1, 'b')
(1, 'c')
(5, 'a')
"""// Usage 1 - Use tuple to store priority and data.
priority_queue<vector<int>,
vector<vector<int>>,
greater<vector<int>>> pq2;
pq2.push({5, 99});
pq2.push({1, 98});
pq2.push({1, 97});
while (!pq2.empty())
{
vector<int> vec = pq2.top();
printf("%d, %d\n", vec[0], vec[1]);
pq2.pop();
}
"""
print:
1, 97
1, 98
5, 99
"""# Usage 2 - Use a class object to store priority and data.
class State:
def __init__(self, priority, data):
self.priority = priority
self.data = data
def __lt__(self, other):
return self.priority < other.priority
pq.put(State(5, 'a'))
pq.put(State(1, 'b'))
while not pq.empty():
state = pq.get()
print(state.priority, state.data) # print (1, 'b') then (5, 'a').// Usage 2 - Use a class object to store priority and data.
struct State {
int priority;
string data;
bool operator<(const State& state) const {
// "greater" comparison gives a min-heap.
return priority > state.priority;
}
};
priority_queue<State> pq;
pq.push(State{5, 'a'});
pq.push(State{1, 'b'});
while (!pq.empty()) {
const State state = pq.top();
pq.pop();
// print (1, 'b') then (5, 'a').
printf("%d, %s\n", state.priority, state.data.c_str());
}